4.27 The Resistance-Distance Matrix
The resistance-distance matrix of a vertex-labeled connected graph G, denoted by Ω, is a real symmetric V × V matrix defined as [266]:
[ Ω] ij= 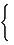 |
ωij if i ≠ j |
| 0 otherwise (82) |
where ωij is resistance-distance between vertices i and j in G.
The resistance-distance matrix was derived on the basis of the theory of resistive electrical networks [164,267]. An electrical network can be presented by a connected graph G in which the vertices of G correspond to unit resistors [12]. The effective resistance between the pairs of vertices is then a graph-theoretical distance, hence the term resistance-distance.
If a graph is acyclic, then [Ω]ij is the sum of resistances (each being equal to one) along the path connecting vertices i and j. On the other hand, if a graph contains cycles, Kirchhoff' laws should be employed to obtain [Ω]ij. Properties of the resistance-distance matrix have been studied by several authors [266,268-276].
As an example, the resistance-distance matrix of the vertex-labeled graph G1 (see structure A in Figure 2) is given below.
Ω(G1)= |
 |
0 |
1 |
2 |
11/4 |
3 |
11/4 |
15/4 |
 |
1 |
0 |
1 |
7/4 |
2 |
7/4 |
11/4 |
2 |
1 |
0 |
3/4 |
1 |
3/4 |
7/4 |
11/4 |
7/4 |
3/4 |
0 |
3/4 |
1 |
2 |
3 |
2 |
1 |
3/4 |
0 |
3/4 |
7/4 |
11/4 |
7/4 |
3/4 |
1 |
3/4 |
0 |
1 |
15/4 |
11/4 |
7/4 |
2 |
7/4 |
1 |
0 |
An algorithm based on the Laplacian matrix has been proposed for efficacious computing of the resistance-distance matrix for connected graphs [277]. This computational algorithm consists of the following steps:
(i) Set up connected graph G with V vertices.
(ii) Construct the Laplacian matrix L for G.
(iii) Set up an auxiliary matrix Φ of G. Matrix Φ is a V × V matrix all of whose elements are equal to one.
(iv) Construct the sum-matrix ξ = [L + x Φ/V] with x having a nonzero arbitrary value bigger than 0. For simple graphs, the value of x is taken to be unity. For the weighted graphs, the value of x differs from unity.
(v) Compute the inverse of the sum-matrix ξ' = 1/[L + x Φ/V]. The inverse is nonsingular for connected graphs.
(vi) Compute the resistance-distance matrix Ω using the elements of the ξ' matrix: [Ω]ij=
[ξ']ii - 2 [ξ']ij+ [ξ']jj.
Application of the algorithm to graph G1 (see structure A in Figure 2) is presented in Chart I.
Chart I. Application of the algorithm for computing the resistance-distance matrix of a simple graph
(i) Graph G1 (see structure A in Figure 2)
(ii) The Laplacian matrix L of G1 (see section 2.15 ).
(iii) The auxiliary matrix Φ of G1
Φ(G1)= |
 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
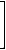 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
(iv) The sum-matrix ξ of G1
ξ(G1)=1/7 |
|
8 |
-6 |
1 |
1 |
1 |
1 |
1 |
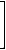 |
-6 |
15 |
-6 |
1 |
1 |
1 |
1 |
1 |
-6 |
22 |
-6 |
1 |
-6 |
1 |
1 |
1 |
-6 |
15 |
-6 |
1 |
1 |
1 |
1 |
1 |
-6 |
15 |
-6 |
1 |
1 |
-6 |
1 |
1 |
-6 |
22 |
-6 |
1 |
1 |
1 |
1 |
1 |
-6 |
8 |
(v) The inverse of the sum-matrix ξ' of G1
ξ'(G1)= |
|
1.59 |
0.73 |
0.02 |
-0.23 |
-0.34 |
-0.31 |
-0.45 |
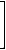 |
0.73 |
0.87 |
0.16 |
-0.09 |
-0.20 |
-0.16 |
-0.31 |
0.02 |
0.16 |
0.44 |
0.19 |
0.09 |
0.012 |
-0.02 |
-0.23 |
-0.09 |
0.19 |
0.69 |
0.34 |
0.12 |
-0.02 |
-0.34 |
-0.20 |
0.09 |
0.34 |
0.73 |
0.27 |
0.12 |
-0.31 |
-0.16 |
0.12 |
0.12 |
0.27 |
0.55 |
0.41 |
-0.45 |
-0.31 |
-0.02 |
-0.02 |
0.12 |
0.41 |
1.27 |
(vi) Compute the resistance-distance matrix Ω of G1
Ω(G1)= |
|
0 |
1 |
2 |
11/4 |
3 |
11/4 |
15/4 |
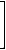 |
1 |
0 |
1 |
7/4 |
2 |
7/4 |
11/4 |
2 |
1 |
0 |
3/4 |
1 |
3/4 |
7/4 |
11/4 |
7/4 |
3/4 |
0 |
3/4 |
1 |
2 |
3 |
2 |
1 |
3/4 |
0 |
3/4 |
7/4 |
11/4 |
7/4 |
3/4 |
1 |
3/4 |
0 |
1 |
15/4 |
11/4 |
7/4 |
2 |
7/4 |
1 |
0 |
The Wiener-like distance index, named the Kirchhoff index [268,275], is based on the resistance-distance matrix.
However, it has been elegantly demonstrated [278] that the
quasi-Wiener index [170,171,279] and the Kirchhoff index are identical topological indices .
<< . . . >>
