The Vertex-Adjacency Matrix, denoted by vA, of a vertex-labeled connected simple graph G with V vertices is a square V × V matrix, which is determined by adjacencies of vertices in G [12].
[vA]ij= |
1 if vertices i and j are adjacent |
| 0 otherwise (1) |
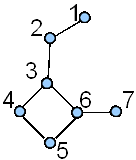
The term vertex-adjacency matrix was first used in chemical graph theory by Mallion in his interesting paper on graph-theoretical aspects of ring current theory [41]. Below we give the vertex-adjacency matrix of the vertex-labeled graph G1 (see structure A in Figure 2).
 A
A 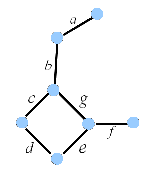 B
B
Figure 2. A vertex-labeled(A) and edge-labeled (B) graph G1
| vA(G1)= | 0 | 1 |
0 |
0 |
0 |
0 |
0 |
||
| 1 | 0 |
1 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
0 |
1 |
0 |
1 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
0 |
0 |
|||
| 0 | 0 |
0 |
1 |
0 |
1 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
0 |
1 |
|||
| 0 | 0 |
0 |
0 |
0 |
1 |
0 |
It is evident that vA is symmetric matrix with a zero diagonal. Therefore, the transpose vAT of the vertex-adjaceny matrix leaves vA unchanged:
vAT = vA (2)
The inverse of the vertex-adjacency matrix vA-1 is defined by:
vA-1 vA = vA vA-1 = I (2a)
where I is V × V unit matrix. vA-1matrix is defined as:
vA-1 = adj vA /det vA (2b)
where adj vA is matrix adjoint to vA. The matrix adjoint to vA can be obtained by first replacing each element [vA]ij by its cofactor in det vA, and then transposing rows and columns. If the vertex-adjacency matrix vA is to have an inverse vA-1, the determinant of vA must not vanish.
If the vertex-adjacency matrix is associated with the graph G composed of two components Ga and Gb:
G = Ga![]() Gb
Gb
then vA has the block-diagram form:
vA(G)= |
[ | vA(Ga) |
0 |
] |
0 |
vA(Gb) |
where 0 are the zero matrices of the size possessed by the components.
A simple yet useful result concerns the vertex-adjacency matrix of bipartite graphs. A bipartite graph G is a graph whose vertex-set V(G) can be partitioned into two nonempty subsets V1 and V2 such that every edge in G connects V1 and V2. Therefore, the first neighbors of vertices in V1 are contained in V2 and vice versa. It should be noted that acyclic graphs are always bipartite. A simple theorem due to König [42] is very helpful for quick determination as to whether a given polycyclic graph is bipartite or not: A graph is bipartite if, and only if, all its cycles are even-membered.
In chemistry, bipartite graphs are used to represent alternant structures. If a bipartite is labeled in such a way that vertices 1,2,...,p belong to the subset V1 and vertices p+1, p+2,..., p+q (=V) are in the subset V2, then the corresponding vertex-adjacency matrix is given by:
| vA(G)= | [ | 0 |
B |
] |
BT |
0 |
where B is a submatrix with dimensions p × q, BT is its transpose and 0 are the zero matrices of the size possessed by the submatrices. The consequence of this result is that eigenvalues of the vertex-adjacency matrix of bipartite graphs are paired [43]. Graph G1 in Figure 1 is an example of the bipartite graph. In Figure 3, we give the labeling of the vertices in G1resulting from splitting its vertices into subsets V1and V2 and below it the corresponding block-diagonal form of the vertex-adjacency matrix of G1.
Figure3. Graph G1 with conveniently labeled vertices to give the vertex-adjacency matrix in the block-diagonal form.
| vA(G1)= | 0 | 0 |
0 |
0 |
1 |
0 |
0 |
||
| 0 | 0 |
0 |
0 |
1 |
1 |
1 |
|||
| 0 | 0 |
0 |
0 |
0 |
1 |
1 |
|||
| 0 | 0 |
0 |
0 |
0 |
0 |
1 |
|||
| 1 | 1 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
1 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
1 |
1 |
0 |
0 |
0 |
The vertex-adjacency matrix vA, the higher order vertex-adjacency matrices vAK (K = 2,3,...) and the higher power vertex-adjacency matrices vAλ (λ=2,3,...) appear to be useful for generating a variety of molecular descriptors [2,21,22,26-28,44-50], but also for other purpose [51-54].
The K-th order vertex-adjacency matrix vAK is defined as:
[vAK ]ij= |
1 if the vertex i is the K-th neighbour of the vertex j |
| 0 otherwise (4) |
| vA2(G1)= | 0 | 0 |
1 |
0 |
0 |
0 |
0 |
||
| 0 | 0 |
0 |
1 |
0 |
1 |
0 |
|||
| 1 | 0 |
0 |
0 |
1 |
0 |
1 |
|||
| 0 | 1 |
0 |
0 |
0 |
1 |
0 |
|||
| 0 | 0 |
1 |
0 |
0 |
0 |
1 |
|||
| 0 | 1 |
0 |
1 |
0 |
0 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
0 |
0 |
The higher power vertex-adjacency matrices vAλ (λ=2,3,...) can be obtained by the matrix-multiplication rules. The squared adjacency matrix vA2 of the vertex-labeled graph G1 (see structure A in Figure 2) is presented below.
vA2(G1)= |
1 | 0 |
1 |
0 |
0 |
0 |
0 |
||
| 0 | 2 |
0 |
1 |
0 |
1 |
0 |
|||
| 1 | 0 |
3 |
0 |
2 |
0 |
1 |
|||
| 0 | 1 |
0 |
2 |
0 |
2 |
0 |
|||
| 0 | 0 |
2 |
0 |
2 |
0 |
1 |
|||
| 0 | 1 |
0 |
2 |
0 |
3 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
0 |
1 |
Walks can be generated from powers of the vertex-adjacency matrix [366]. A walk in a graph is an alternating sequence of vertices and edges, such that each edge begins and ends with the vertices immediately preceding and following it [12]. The self-returning walk is a walk that starts and ends at the same vertex.
Figure 4. All self-returning walks of length 2 on G1 (see structure A in Figure 2)
The length of the walk is the number of edges contained in it. Repetition of vertices and/or edges is allowed in a walk. The number of walks of length λ beginning at vertex i and ending at vertex j is given by the i, j-element of the λ-th power of the vertex-adjacency matrix: [ vAλ ]ij. The number of self-returning walks of length λ is given by i, i-element of the λ-th power of the vertex-adjacency matrix: [ vAλ ]ii. Walks have been extensively applied, for example, as measures of the complexity graphs, molecules and surfaces [48,55-62] and for discrimination and ordering of chemical structures [63]. All self-returning walks and all walks of length 2 on G1 are respectively illustrated in Figures 4 and 5 .
Figure 5 . All walks of length 2 on G1 (see structure A in Figure 2)
The permanent of the vertex-adjacency matrix per vA can be used to enumerate the number of Kekulé structures K (or in the graph-theoretical terminology 1-factors [12,19] or dimers [19]) of alternant structures [64-68]:
per vA = (K)2 (5)
Many topological indices are based on the vertex-adjacency matrix, e.g., the total vertex-adjancecy index [69], the Narumi simple topological index [70], the Zagreb indices [71-78, 367,370], the vertex-connectivity index [79-85,368], overall connectivity indices [69,369], the Gordon-Scantlebury index [44,86], the Platt index [44,86], the leading eigenvalue of the vertex-adjacency matrix [88], or the walk-count indices [45-52,54-57,369,370].