4.1 The Standard or Vertex-Distance Matrix
The standard distance matrix or the vertex-distance matrix (or the minimum path matrix) of a vertex-labeled connected graph G [2,12,18,26,193], denoted by vD, is a real symmetric V × V matrix whose elements are defined as:
[ vD] ij= 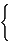 |
l(i,j) if i ≠ j |
| 0 otherwise (45) |
where l(i,j) is the length of the shortest path, i.e., the minimum number of edges, between vertices i and j in G. The length l(i,j) is also called the distance [194-197] between vertices i and j in G,
hence the term distance matrix. The term matrix of lengths for the distance matrix has also been used [198]. The shortest distance between two vertices in a graph is also called the geodesic distance [12].
The standard distance matrix of the vertex-labeled graph G1 (see structure A in Figure 2) is as follows:
vD(G1)= |
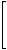 |
0 |
1 |
2 |
3 |
4 |
3 |
4 |
 |
1 |
0 |
1 |
2 |
3 |
2 |
3 |
2 |
1 |
0 |
1 |
2 |
1 |
2 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
2 |
1 |
2 |
1 |
0 |
1 |
4 |
3 |
2 |
3 |
2 |
1 |
0 |
We also give here the vertex-distance matrix of T2, since we will use this particular matrix later on.
vD(T2)= |
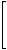 |
0 |
1 |
2 |
3 |
4 |
5 |
3 |
2 |
 |
1 |
0 |
1 |
2 |
3 |
4 |
2 |
1 |
2 |
1 |
0 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
1 |
0 |
1 |
2 |
2 |
3 |
4 |
3 |
2 |
1 |
0 |
1 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
0 |
4 |
5 |
3 |
2 |
1 |
2 |
3 |
4 |
0 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
3 |
0 |
An efficient algorithm is available for computing the vertex-distance matrix of any graph [199]. This matrix has been used to generate a number od topological indices, e.g., the Wiener index [21,25,200-205], the multiplicative Wiener index [206-208], the hyper-Wiener index [209-212], the Balaban index [213,214], and the distance-sum index [215,277].
Hosoya et al. [216,217] observed that two non-isomorphic graphs may possess identical distance-spectra. We already mentioned isospectral graphs when presenting the Hückel matrix (see section 2.14). A pair of the two polyhedral graphs that possess the same distance-spectra are shown in Figure 30.
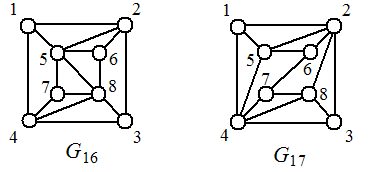
Figure 30. A pair of graphs possessing identical distance-spectra. These two polyhedral graphs are Schlegel graphs representing the pair of nonahedra.
Their vertex-distance matrices are given as follows:
vD(G16)= |
 |
0 |
1 |
2 |
1 |
1 |
2 |
2 |
2 |
 |
1 |
0 |
1 |
2 |
1 |
1 |
2 |
2 |
2 |
1 |
0 |
1 |
2 |
2 |
2 |
1 |
1 |
2 |
1 |
0 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
0 |
1 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
0 |
2 |
1 |
2 |
2 |
2 |
1 |
1 |
2 |
0 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
0 |
vD(G17)= |
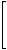 |
0 |
1 |
2 |
1 |
1 |
2 |
2 |
2 |
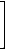 |
1 |
0 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
1 |
0 |
1 |
2 |
2 |
2 |
1 |
1 |
2 |
1 |
0 |
1 |
2 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
0 |
1 |
2 |
2 |
2 |
2 |
1 |
2 |
1 |
0 |
1 |
2 |
1 |
1 |
1 |
2 |
2 |
1 |
0 |
The corresponding distance-spectra are identical: {G16} = {G17} = {10.3150, 0.2985, 0.0953, -0.8112, -1.2624, -2.4773, -2.8024, -3.3557}.
These kind of graphs are called twin graphs [216] because besides identical distance spectra and consequently identical distance-polynomials, they possess identical characteristic polynomials and their spectra {3.8801, 1.3557, 0.7732, 0.4773, -0.7376, -1.2464, -2.0953, -2.4069}, identical matching polynomials and their spectra, and many identical graph-theoretical invariants.
<< . . . >>

