 G6
G6 The Hückel matrix, encountered in the Hückel theory of conjugated systems [138-140] may be considered to be an augmented vertex-adjacency matrix [2]. In the Hückel theory, it is wished to solve the following secular equation set up for a given conjugated system [141] :
det |-ei S + H| = 0; i=1,…,V (21)
where H is the Hamiltonian matrix, S is the overlap matrix, ei is the set of eigenvalues and V is the number of π-electrons in a conjugated molecule. The Hamiltonian matrix and the overlap matrix in the Hückel theory are simplified by using the set of approximations originally introduced by Bloch [142,143], but known in the quantum-chemical literature as the Hückel approximations [141]:
H = αI + β vA (22)
S = I (23)
where I is the unit V × V matrix, α is an atomic parameter (atomic Coulomb integral), β is a bond parameter (resonance integral) and vA is the vertex-adjacency matrix.
Introducing (22) and (23) into (21), we obtain:
det | (-ei + α ) I + β vA | = 0; i=1,…,V (24)
where the ei are the Hückel eigenvalues. If β is used as the unit of energy and α as the zero-reference point, then the determinant (24) reduces to:
det | (-ei) I + vA | = 0; i=1,…,V (25)
Hence, the Hückel matrix X is kind of augmented vertex-adjacency matrix:
X = -ei I + vA; i =1,...,V (26)
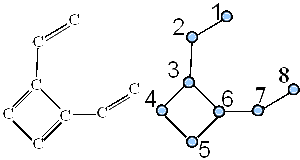
In Figure 18, we give graph G6 representing the carbon skeleton of 1,2-divinyl cyclobutadiene.
Figure 18. Graph G6 representing the carbon skeleton of 1,2-divinylcyclobutadiene.
The corresponding Hückel matrix is given by:
X(G6)= |
-e | 1 |
0 |
0 |
0 |
0 |
0 |
0 |
||
| 1 | -e |
1 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
-e |
1 |
0 |
1 |
0 |
0 |
|||
| 0 | 0 |
1 |
-e |
1 |
0 |
0 |
0 |
|||
| 0 | 0 |
0 |
1 |
-e |
1 |
0 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
-e |
1 |
0 |
|||
| 0 | 0 |
0 |
0 |
0 |
1 |
-e |
1 |
|||
| 0 | 0 |
0 |
0 |
0 |
0 |
1 |
-e |
In the early days of quantum chemistry, before the age of computers, the Hückel theory was widely used, but in spite of its simplicity it is still in use, e.g., papers appear continually in Physics Reviews B using the Hückel theory in a solid-state 'tight-binding' format. The Hückel theory also plays a central role in a recent paper by Klein and Misra in their discussion of minimally Kekulenoid π–networks and reactivity of acyclics [144]. Additionally, graph-theoretical analysis of the Hückel theory [e.g .,145-148] has provided elegant answers to some questions that were previously left unanswered, such as why only a few (six to be precise [149]) conjugated molecules have only integers as eigenvalues or why some structurally quite different molecules possess identical sets of eigenvalues (that is, identical Hückel spectra) [150-158], etc. Graphs with identical spectra are called isospectral or cospectral graphs. For example, in Figure 19 we give graphs G7 and G8 of two structurally-different molecules - 1,4 - divinylbenzene and 2-phenylbutadiene - that possess identical Hückel spectra. Their vertex-adjacency matrices are given below the figure.
Figure 19. A classical example of a pair of isospectral graphs.
X(G7)= |
0 | 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
| 1 | 0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|||
| 0 | 0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|||
| 0 | 0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|||
| 0 | 0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |||
| 0 | 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
X(G8)= |
0 | 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
| 1 | 0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| 0 | 0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|||
| 0 | 0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|||
| 0 | 0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |||
| 0 | 0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
The corresponding Hückel spectra are identical: {G7} = {G8} = { ±2.2143, ±1.6751, ±1.0000, ±1.0000, ±0.5392 } .