5.10 The Cluj Matrices
The Cluj matrix is a square unsymmetrical V × V matrix, denoted by uC, whose elements are defined as [218,311-315]:
[ uC] ij= 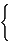 |
Vi,p(ij) if i ≠ j |
0 otherwise (101) |
where Vi,p(ij) is determined from the subgraph G-(p(i,j)) remaining when the edges and any internal vertices of the path p(i,j) are deleted from G. Then Vi,p(ij) is the number of vertices closer to i than j in the component of G-(p(i,j)) containing i. The unsymmetric Cluj matrix can be constructed for any connected graph. In the case of graphs containing cycles, there can exist several shortest paths. Among them, one selects that path which allows the maximum value of Vi,p(ij).
The unsymmetric Cluj matrix for G1 (see structure A in Figure 2) is as follows:
uC(G1)= |
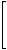 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
 |
6 |
0 |
2 |
2 |
2 |
2 |
2 |
5 |
5 |
0 |
5 |
3 |
4 |
4 |
4 |
2 |
2 |
0 |
4 |
1 |
4 |
3 |
3 |
1 |
3 |
0 |
2 |
2 |
4 |
3 |
3 |
2 |
5 |
0 |
6 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
The unsymmetric Cluj matrix for the branched tree T2 is given below.
uC(T2)= |
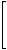 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
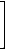 |
7 |
0 |
3 |
3 |
3 |
3 |
3 |
7 |
5 |
5 |
0 |
5 |
5 |
5 |
7 |
5 |
3 |
3 |
3 |
0 |
6 |
6 |
3 |
3 |
2 |
2 |
2 |
2 |
0 |
7 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
The unsymmetrical Cluj matrix uC may be symmetrized to give the path-Clujmatrix pC and the edge-Cluj matrix eC:
pC = uC • uCT (102)
eC = pC • vA (103)
where the symbol • denotes the Hadamard matrix product [285] and uCT is the transpose of uC.
The Hadamard matrix product of two matrices A and B of the same dimensions is defined as:
[A • B]ij= [A]ij[B]ij (104)
It should be noted that for acyclic graphs the pC and eC matrices are identical to the pW and eW matrices, respectively.
For cycle-containing graphs, the eC matrix is equal to the edge-Szeged matrix [270]:
eC = eSZ (105)
while the pC matrix differs from any previously known special matrix based on paths.
Below we give the path-Cluj matrix of G1.
pC(G1)= |
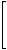 |
0 |
6 |
5 |
4 |
3 |
4 |
1 |
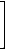 |
6 |
0 |
10 |
4 |
6 |
6 |
2 |
5 |
10 |
0 |
10 |
3 |
12 |
4 |
4 |
4 |
10 |
0 |
12 |
2 |
4 |
3 |
6 |
3 |
12 |
0 |
10 |
2 |
4 |
6 |
12 |
2 |
10 |
0 |
6 |
1 |
2 |
4 |
4 |
2 |
6 |
0 |
<< . . . >>
