5.7 Szeged Matrices
Several Szeged matrices have been proposed in the literature [306]. Here, we will consider the edge-Szeged matrix, the path-Szeged matrix and the Szeged difference matrix. The edge-Szeged matrix, denoted by eSZ, was introduced by Gutman [205]. It is formally defined as the Wiener matrix:
[ eSZ] ij= 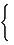 |
Vi,e Vj,e if i ≠ j |
| 0 otherwise (97) |
where Vi,e and Vj,e now denote the numbers of vertices lying closer to i and to j, respectively, whilst the vertices equidistant to i and j are not counted. A consequence of the formal identity between (90) and (97) is that the edge-Wiener matrices and the edge-Szeged matrices are identical for acyclic graphs. Therefore, the edge-Szeged matrix may be regarded as the extension of the edge-Wiener matrix to cycle-containing graphs. To illustrate this, we give below the edge-Szeged matrix for the graph G1 (see structure A in Figure 2).
eSZ(G1)= |
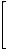 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
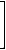 |
6 |
0 |
10 |
0 |
0 |
0 |
0 |
0 |
10 |
0 |
10 |
0 |
12 |
0 |
0 |
0 |
10 |
0 |
12 |
0 |
0 |
0 |
0 |
0 |
12 |
0 |
10 |
0 |
0 |
0 |
12 |
0 |
10 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
The summation of elements in the upper or lower matrix-triangle produces the Szeged index [307-310] .
Diudea et al. [306] introduced the path-Szeged matrix, denoted by pSZ. The above definition for the edge-Szeged matrix is extended to the path-Szeged matrix by consideration of the paths instead of the edges in G. Now the pSZ matrix is no longer identical to the pW matrix as can be seen by comparing these two matrices for T2.
The path-Szeged matrix for T2 is given below.
pSZ(T2)= |
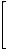 |
0 |
7 |
5 |
15 |
9 |
15 |
15 |
1 |
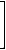 |
7 |
0 |
15 |
9 |
15 |
10 |
3 |
7 |
5 |
15 |
0 |
15 |
10 |
12 |
7 |
5 |
15 |
9 |
15 |
0 |
12 |
6 |
3 |
15 |
9 |
15 |
10 |
12 |
0 |
7 |
15 |
9 |
15 |
10 |
12 |
6 |
7 |
0 |
10 |
15 |
15 |
3 |
7 |
3 |
15 |
10 |
0 |
15 |
1 |
7 |
5 |
15 |
9 |
15 |
15 |
0 |
We also give the path-Szeged matrix for
G1 (see structure
A in
Figure 2).
pSZ(G1)= |
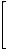 |
0 |
6 |
5 |
10 |
8 |
10 |
6 |
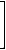 |
6 |
0 |
10 |
4 |
12 |
6 |
12 |
5 |
10 |
0 |
10 |
3 |
12 |
4 |
10 |
4 |
10 |
0 |
12 |
2 |
10 |
8 |
12 |
3 |
12 |
0 |
10 |
2 |
10 |
6 |
12 |
2 |
10 |
0 |
6 |
6 |
12 |
4 |
10 |
2 |
6 |
0 |
The summation of elements in the upper or lower matrix-triangle produces the hyper-Szeged index [21] .
The Szeged difference matrix, denoted by dSZ, is defined as the difference of the edge- and path-Szeged matrices:
dSZ = pSZ – eSZ (98)
The Szeged difference matrices for T2 and G1 (see structure A in Figure 2) is exemplified below.
dSZ(T2)= |
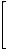 |
0 |
0 |
5 |
15 |
9 |
15 |
15 |
1 |
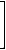 |
0 |
0 |
0 |
9 |
15 |
10 |
3 |
0 |
5 |
0 |
0 |
0 |
10 |
12 |
0 |
5 |
15 |
9 |
0 |
0 |
0 |
6 |
3 |
15 |
9 |
15 |
10 |
0 |
0 |
0 |
15 |
9 |
15 |
10 |
12 |
6 |
0 |
0 |
10 |
15 |
15 |
3 |
0 |
3 |
15 |
10 |
0 |
15 |
1 |
0 |
5 |
15 |
9 |
15 |
15 |
0 |
dSZ(G1)= |
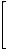 |
0 |
0 |
5 |
10 |
8 |
10 |
6 |
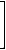 |
0 |
0 |
0 |
4 |
12 |
6 |
12 |
5 |
0 |
0 |
0 |
3 |
0 |
4 |
10 |
4 |
0 |
0 |
0 |
2 |
10 |
8 |
12 |
3 |
0 |
0 |
0 |
2 |
10 |
6 |
0 |
2 |
0 |
0 |
0 |
6 |
12 |
4 |
10 |
2 |
0 |
0 |
<< . . . >>
