4.13 The Complementary Vertex-Distance Matrix
The complementary vertex-distance matrix, denoted by cvD, has been introduced by Ivanciuc [234] and discussed by Balaban et al.[221] and Ivanciuc et al. [236]. It is a square symmetric V × V matrix defined as:
[cvD]ij= 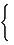 |
lmin+ lmax - [vD]ij if i ≠ j |
| 0 otherwise (62) |
where lminand lmax are the minimum and the maximum distance in a graph.
If a graph is simple, than lmin = 1 and lmax = the graph diameter D and the complementary vertex-distance matrix (62) becomes:
[ cvD] ij= 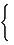 |
1 + D - [vD]ij if i ≠ j |
| 0 otherwise (63) |
The diameter D of a graph G is the longest geodesic distance between any two vertices i and j in G, i.e.,the largest [vD]ij value in the vertex-distance matrix [12]. The elements of the complementary-distance matrix differ from the elements of the reverse-Wiener matrix only for unity (see section 5.5).
The complementary vertex-distance matrices of T2and G1 (see structure A in Figure 2) are as follows:
cvD(T2)= |
 |
0 |
5 |
4 |
3 |
2 |
1 |
3 |
4 |
 |
5 |
0 |
5 |
4 |
3 |
2 |
4 |
5 |
4 |
5 |
0 |
5 |
4 |
3 |
5 |
4 |
3 |
4 |
5 |
0 |
5 |
4 |
4 |
3 |
2 |
3 |
4 |
5 |
0 |
5 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
0 |
2 |
1 |
3 |
4 |
5 |
4 |
3 |
2 |
0 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
3 |
0 |
cvD(G1)= |
 |
0 |
4 |
3 |
2 |
1 |
2 |
1 |
 |
4 |
0 |
4 |
3 |
2 |
3 |
2 |
3 |
4 |
0 |
4 |
3 |
4 |
3 |
2 |
3 |
4 |
0 |
4 |
3 |
2 |
1 |
2 |
3 |
4 |
0 |
4 |
3 |
2 |
3 |
4 |
3 |
4 |
0 |
4 |
1 |
2 |
3 |
2 |
3 |
4 |
0 |
The complementary vertex-distance matrices are used to generate the Wiener-like molecular descriptors
that have been successfully tested in QSPR modeling
[236]. The complementary vertex-distance matrices
of vertex- and edge-weighted graphs
have also been introduced and used in
QSPR [234].
<< . . . >>
