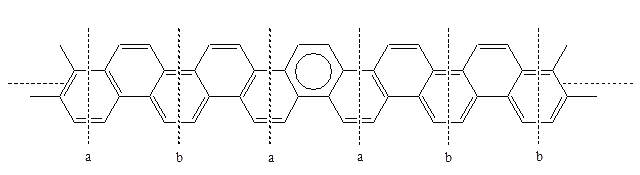
The transfer matrix, denoted by T, is a very useful matrix for computing the number of Kekulé structures (1-factors, dimers) of long strips with repeating units (unit cells) such as polymeric chains or cage structures such as fullerenes that are built up by fusing several symmetry-equivalent units [2,19,37,340-347]. A diagram of a polyphenanthrene strip is given in Figure 42.
The elements of the transfer matrix represent the propagation of a Kekulé structure from a position at one side of a unit cell to the other side of the cell. When the different possible local features of the Kekulé structures at the boundary of a cell are indicated, the local structure at each boundary is specified. In Figure 42, the local structures are at each of the positions marked by a transverse broken line. At these positions there are only two types of local structures possible, labeled by a and b. The final step to establish the structure of the transfer matrix involves the determination of the number of ways to propagate from one local structure to another at the unit-cell boundary.

Figure 42. A piece of the polyphenanthrene strip and the corresponding local structures.
If we consider the polyphenanthrene strip given in Figure 42, it is seen that at a position immediately following a local structure a there can occur either two a local structures (because the number of Kekulé structures for the benzene ring separating two a local structures is 2) or a single b local structure. In the case of a local structure b there can at the position immediately following it occur either a or b local structures. This can be summarized as:
a => 2a + b (126)
b => a + b (127)
If KL(a) or KL(b) denotes the number of Kekulé structures for a polyphenanthrene strip with length L and with local structures a (or b) at the terminal end, then:
KL+1(a) = 2 KL(a) + KL(b) (128)
KL+1(b) = KL(a) + KL(b) (129)
and after setting up the transfer matrix T:
T= |
2 |
1 |
||
1 |
1 |
it follows that:
KL+1(a) |
= T |
KL(a) |
= TL |
K1(a) |
(130) |
||||||
KL+1(b) |
KL(b) |
K1(b) |
The final counting formula is given by:
K = [2 1]TL |
1 |
(131) |
||
1 |
Then, the standard matrix multiplication produces the number of Kekulé structures. For example, the number of Kekulé structures for the polyphenanthrene strip of length 6 is 987.
The transfer matrix was also used to enumerate [348-351] the conjugated circuits [352-355] of conjugated polymers, fullerenes, nanotubes, and even graphite. The transfer-matrix method can be used further to enumerate a great variety of subgraph structures, especially for regularly repeating polymeric or quasi-one-dimensional parent graphs. As a number of researchers have shown, this includes matchings, self-avoiding walks, characteristic polynomials (i.e., weighted Sachs subgraphs [2]), resonance-theoretic subgraphs, and rather general Ising-type-model subgraphs. Even further much the same idea applies [356] in treating coupled differential equations on suitable quasi-one-dimensional systems.