5.17 The Random-Walk Markov Matrix
A random walk in a (molecular) graph is naturally designated by a probability measure, of which there are at least two natural intrinsic examples. The first is the probability measure that entails starting walks from each vertex with equal probability and taking subsequent steps such that each neighbouring vertex is reached with equal probability, so that the probabilty of stepping from one vertex to another vertex is 1/d, where d is the vertex-degree. The walks of the consequently generated distribution are referred to [333] as simple random walks. The second is the probability measure that takes each possible walk of a given length as equally probable. These probability measures are generally quite different, though if a graph is regular, i.e., having all vertices of the same degree, then the two probability measures are equivalent. The walks generated by this second probability measure are called equipoise random walks [334]. The simple random walks have rarely been used in chemical graph theory [e.g., 335,336], whereas the equipoise random walks have been used more often [e.g., 45-57]. Often either equipoise or simple random walks have been called just random, probably without recognition of the alternative type – or perhaps as a result of confusion of the two possibilities.
Walks can be generated from powers of the vertex-adjacency matrix vA (see section 2.1), and this may be viewed as an identification of the distribution for equipoise random walks. Similarly, the distribution for simple random walks can be generated by powers of a Markov matrix. The random-walk Markov matrix, denoted by MM, of a vertex-labeled connected graph G is a real unsymmetrical V × V matrix whose elements are probabilities for the associated individual steps [334] :
[ MM] ij= 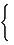 |
1/[d(j)] if i ≠ j |
| 0 otherwise (119) |
Then [MMλ]ij is the probability for a λ-step random walk beginning at vertex j and ending at vertex i.
The random-walk Markov matrix of the vertex-labeled graph G1 (presented in Figure 2) is as follows:
MM(G1)= |
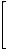 |
0 |
1/2 |
0 |
0 |
0 |
0 |
0 |
 |
1 |
0 |
1/3 |
0 |
0 |
0 |
0 |
0 |
1/2 |
0 |
1/2 |
0 |
1/3 |
0 |
0 |
0 |
1/3 |
0 |
1/2 |
0 |
0 |
0 |
0 |
0 |
1/2 |
0 |
1/3 |
0 |
0 |
0 |
1/3 |
0 |
1/2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1/3 |
0 |
The Markov matrix MM may be also expressed in terms of the vertex-adjacency matrix vA and the inverse diagonal matrix Δ:
MM = vA Δ-1 (120)
Several unsymmetrical graph-theoretical matrices such as the Cluj matrices (see section 5.7) and the layer matrices [337] have also been proposed. However, the Markov matrix has a much wider field of application [ e.g ., 338]. It should be noted that the (simple) random walks have been extensively studied in mathematics and physics [333] but only occasionally in chemistry as has already been noted.
Algebraic manipulations with the Markov matrix appear to be rewarding in chemical graph theory. For example, the combination of the Markov matrix MM and the diagonal matrix Δ1/2 with elements:
[Δ1/2]ii = [d(i)]1/2 (121)
and its inverse Δ-1/2, gives the following symmetric matrix:
Γ = Δ-1/2 MM Δ1/2 (122)
As an example, we give the matrix Γ of the vertex-labeled graph G1 (see structure A in Figure 2).
MM(G1)= |
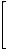 |
0 |
1/√2 |
0 |
0 |
0 |
0 |
0 |
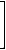 |
1/√2 |
0 |
1/√6 |
0 |
0 |
0 |
0 |
0 |
1/√6 |
0 |
1/√6 |
0 |
0 |
0 |
0 |
0 |
1/√6 |
0 |
1/2 |
0 |
0 |
0 |
0 |
0 |
1/2 |
0 |
1/√6 |
0 |
0 |
0 |
0 |
0 |
1/√6 |
0 |
1/√3 |
0 |
0 |
0 |
0 |
0 |
1/√3 |
0 |
Matrix Γ is interesting for at least two reasons [334]. The first reason is that the half-sum of elements of the Γ matrix gives the connectivity index χ [79] :
χ = (1/2)∑i ≠ j (Γ)ij (123)
thus, allowing the interpretation of this molecular descriptor as a sum of symmetrized neighbor-hopping probabilities. The second is that it leads to the (standard or combinatorial) Laplacian matrix L:
L = Δ1/2 (I - Γ ) Δ1/2 (124)
while the matrix I- Γ is sometimes called the 'analytic' or normalized Laplacian matrix [339] . If we denote this normalized Laplacian matrix by Lnorm, the connectivity index χ can also be expressed in terms of its elements:
χ = (1/2)∑i ≠ j (Lnorm)ij (125)
<< . . . >>
