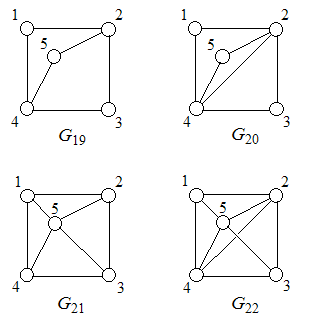The detour matrix (or the maximum path matrix) of a vertex-labeled connected graph G, denoted by DM, is a real symmetric V × V matrix whose elements are defined as [12,18,237,238]:
[DM]ij=  |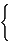
L (i,j) if i ≠ j |
| 0 otherwise (65) |
where L(i,j) is the length of the longest distance, i.e., the maximum number of edges, between vertices i and j. The longest distance in a graph is called the elongation and its length is equal to the detour distance, hence the term detour matrix. It is also convenient to call the longest path connecting the vertices i and j the detour-path.
The detour matrix of the vertex-labeled graph G1 (see structure A in Figure 2) is:
DM(G1)= |
 |
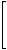0 |
1 |
2 |
5 |
4 |
5 |
6 |
 |
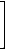1 |
0 |
1 |
4 |
3 |
4 |
5 |
|||
2 |
1 |
0 |
3 |
2 |
3 |
4 |
|||
5 |
4 |
3 |
0 |
3 |
2 |
3 |
|||
4 |
3 |
2 |
3 |
0 |
3 |
4 |
|||
5 |
4 |
3 |
2 |
3 |
0 |
1 |
|||
6 |
5 |
4 |
3 |
4 |
1 |
0 |
Rücker and Rücker [239] proposed a slightly different definition of the detour matrix. These authors pointed out that it was never well-explained either by Harary [12] or others [e.g ., 237] why zeros should appear as diagonal elements of the detour matrix. They therefore defined the diagonal elements of the detour matrix [RRDM]ij as the lengths of the shortest self-returning walks (ssrw) which visit all sites:
[RRDM]ij= |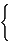
L(i,j) if i ≠ j |
| ssrw(i,i) if i = j (66) |
Thus, the above detour matrix of the vertex-labeled graph G1 (see structure A in Figure 2) becomes:
RRDM(G1)= |
|
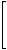10 |
1 |
2 |
5 |
4 |
5 |
6 |
|
1 |
10 |
1 |
4 |
3 |
4 |
5 |
|||
2 |
1 |
10 |
3 |
2 |
3 |
4 |
|||
5 |
4 |
3 |
10 |
3 |
2 |
3 |
|||
4 |
3 |
2 |
3 |
10 |
3 |
4 |
|||
5 |
4 |
3 |
2 |
3 |
10 |
1 |
|||
6 |
5 |
4 |
3 |
4 |
1 |
10 |
where the diagonal elements represent the self-returning walks of length 10, which include visits to all the vertices in G1.
While the standard distance matrix determines a graph uniquely, this is not the case with detour matrix - there exists nonisomorphic graphs with identical detour matrices. Two pairs of such graphs, taken from Randić et al . [240], are shown in Figure 33.
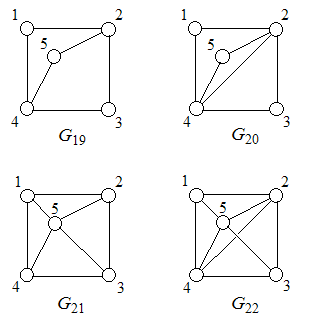
Figure 33. Two pairs of nonisomorphic graphs, G19- G20 and G21- G22, with identical detour matrices.
The detour matrices belonging to the pairs of graphs in Figure 33 are given below.
DM(G19)=DM(G20)= |
|
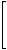0 |
3 |
4 |
3 |
4 |
|
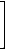3 |
0 |
3 |
2 |
3 |
|||
4 |
3 |
0 |
3 |
4 |
|||
3 |
2 |
3 |
0 |
3 |
|||
4 |
3 |
4 |
3 |
0 |
DM(G21)=DM(G22)= |
|
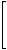0 |
4 |
4 |
4 |
4 |
|
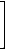4 |
0 |
4 |
4 |
4 |
|||
4 |
4 |
0 |
4 |
4 |
|||
4 |
4 |
4 |
0 |
4 |
|||
4 |
4 |
4 |
4 |
0 |
Several methods are available for computing the detour matrix.We list here three methods:
We present here the second method by which the detour matrix of a polycyclic graph can be generated from the vertex-distance matrices of the corresponding spanning trees following the procedure consisting of the three steps outlined below [238,243,244]:
We illustrate this procedure by considering graph G1. Its vertex-labels are given as structure A in Figure 2. G1 can have only four spanning trees – they are presented in Figure 20. Vertex-distance matrices belonging to spanning trees from Figure 20 are listed below.
Matching these four vertex-distance matrices and choosing the appropriate elements leads to the detour matrix of G1 that was presented above. It should be also pointed out that the vertex-distance matrix and the detour matrix are identical for acyclic graphs.
The detour matrix was used to generate a Wiener-like index [237], named the detour index [245], for simple and weighted graphs[237,238,241-245]. All kinds of distance indices can be generated from the detour matrix [21,224,245-248].
